归并排序
归并排序
0x00 有序子列的归并
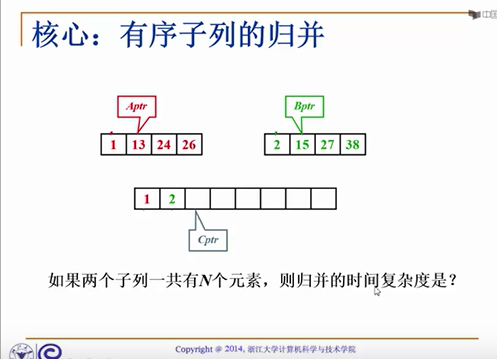
有序子列的归并和之前的多项式求和一样,一共三个指针,两个指向有序子序列,一个用于指向用于临时保存的Temp数组
void merge(ElementType A[],ElementType TempA[],int L,int R,int REnd){
int LEnd=R-1;
int temp=L;
int numElements=REnd-L+1;
while(L<=LEnd&&R<=REnd){
if(A[L]<=A[R]){
TempA[temp++]=A[L++];
}else{
TempA[temp++]=A[R++];
}
}
while(L<=LEnd){
TempA[temp++]=A[L++];
}
while(R<REnd){
TempA[temp++]=A[R++];
}//注意由于时temp++,到这里时temp实际上比REnd大1,所以下面只用REnd,万一不小心使TempA越界,那么free的时候会报错!
while(numElements--){
A[REnd]=TempA[REnd];
REnd--;
}//对于递归实现,每一次都要把merge后的结果从tempa里复制回来,而下面的非递归就不用了
}
0x01 递归实现
void MSort(ElementType A[],ElementType TempA[],int L,int REnd){
int Center;
if(L<REnd){
Center=(L+REnd)/2;
MSort(A,TempA,L,Center);
MSort(A,TempA,Center+1,REnd);
merge(A,TempA,L,Center+1,REnd);
}
}
void Merge_sort1(ElementType A[],int N){
int* TempA=(int*)malloc(sizeof(int)*N);
if(TempA!=NULL){
MSort(A,TempA,0,N-1);
}else{
printf("空间不足!");
}
free(TempA);
}
时间复杂度为nlogn,不在merge函数里malloc TempA,不然会递归的调用很多次,产生很多TempA,然后又free,效率低,所以我们在Merge_sort里一次开一个最大的。
0x02 非递归实现
void Merge_pass(ElementType A[],ElementType TempA[],int N,int length){
int i,j;
for(i=0;i<=N-2*length;i+=2*length)//只能到N-2*length了,因为可能有时剩余的待排序列长度不带2*length个
merge(A,TempA,i,i+length,i+2*length-1);
if(i+length<N)//说明还可以分成两个子序列,只不过第二个子序列长度不到length
merge(A,TempA,i,i+length,N-1);//第REnd为N-1了
else
for(j=i;j<N;j++) TempA[j]=A[j];//否则剩余长度只够一个有序子序列,那就直接复制到TempA里
}
void Merge_sort(ElementType A[],int N){
int length=1;
int* TempA=(int*)malloc(sizeof(int)*N);
if(TempA!=NULL){
while(length<N){
Merge_pass(A,TempA,N,length);
length*=2;
Merge_pass(TempA,A,N,length);
length*=2;
}//用两次merge_pass 和length*2是为了最后数据还返回到A里;即使在某一次循环的第一次merge_pass中length已经到了N/2了也不用担心下一步的length太大导致只够分出一个完整的有序序列,我们的merge_pass对这个情况有处理
free(TempA);
}
else printf("空间不足");
}
归并排序需要额外的O(n)空间复杂度,常用于外部排序,以上代码测试通过!
