希尔排序

0x00 什么是希尔排序

希尔排序利用了插入排序的简单，同时又克服了插入排序每次只交换相邻两个元素的缺点。

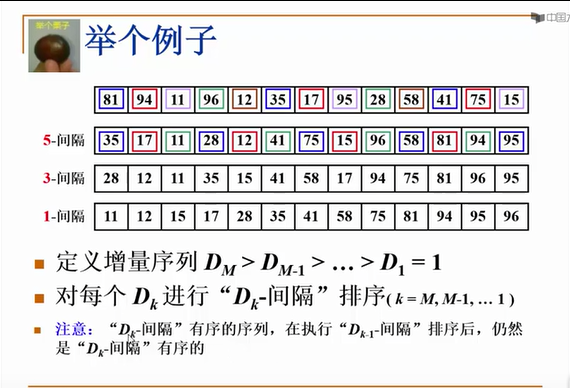
QQ截图20200211122056

插入排序实现起来简单，就是每次插一个元素，然后往前一个一个比较，而希尔排序则是多次插入排序，每次往前比较的距离不同，比如对于上图的例子，一开始是距离为5，所以第一个元素直接从下标为5的开始（普通插入是从1开始），然后往前比较（距离为5），如果比前面小就交换，然后同样的开始插入下一个元素，一只插到最后一个，这是第一次插入排序，下一次则距离为3。之所以能这么做就是因为，先执行的插入排序，不会因后执行的插入排序受到影响而变得无序。

我们把这个间隔的选取称作增长序列，原始的增长序列是

QQ截图20200211123103

由于前面的距离是后面的倍数，所以容易造成下面这种情况：

QQ截图20200211123245

上面这个例子中，初始序列在距离为2时已经符合顺序了，所以用他的倍速做距离毫无意义，只有在最后1的时候才能有效排序。

因此要选择互质的增长序列：

QQ截图20200211123446

0x01 代码实现

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define maxsize 10000000
void traversal(int * data,int n){
	int i;
	for(i=0;i<n;i++){
		printf("%d\t",data[i]);
	}
	printf("\n");
}
int shell_sort(int* data,int n){
	int ret;
	int i,j,k;
	int data1[]={1, 5, 19, 41 ,109 ,209 ,505 ,929 ,2161 ,3905, 8929, 16001 ,36289 ,\
	64769 ,146305, 260609, 587521 ,1045505 ,2354689 ,4188161 };//sedgewich增长序列
	for(k=19;k>=0;k--){
	
		int len=data1[k];
		for(i=len;i<n;i++){//插入排序
			int temp=data[i];
			for(j=i;j>=len&&temp<data[j-len];j-=len){//注意j>=len,因为前面要有元素可以比较j-len>=0
				data[j]=data[j-len];
			}
			data[j]=temp;
		}
	}
	return ret;
}

int main(){
	srand(time(0));
	int i;
	int*data=(int*)malloc(sizeof(int)*maxsize);
	for(i=0;i<maxsize;i++){
		data[i]=rand()*rand();
	}
	shell_sort(data,maxsize);
	traversal(data,10000);
	return 0;
} 

该代码在1000w个int排序时只花费6s，通过多次实验，接近O(n)