快速排序
快速排序
0x00 传说中最快的排序算法
大多数情况下,快速排序的性能相当强悍。与归并排序思想差不多都是分而治之。
1 选一个元素做主元(pivot),将原来的集合分为两大块,左边的集合小于主元,右边的大于主元
2 递归的处理左边集合和右边集合
3 将左边 主元 右边 构成一个集合,就完成了
伪代码描述如下

细节之处 1如何选出主元 2怎么分成独立子集
0x01 选主元
如果选出的主元能够将集合分成等大的两个 就是最好情况 ,反之 每次产生一个空集一个n-1元素的集合时间复杂度最坏,时间复杂度为O(N^2) 下图就是一个例子
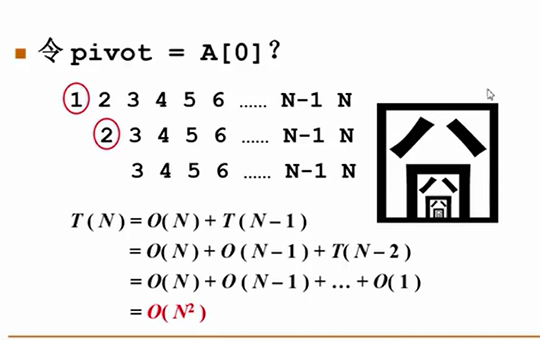
但是刻意选出所有元素的中位数,是一件很复杂的事,所以改进了,取头中尾的中位数(一般)

这个函数能从头中尾三个位置返回中位数,同时将集合进行交换,L<CENTER<R,并且将中与R-1进行交换(原因在于现在的中间位置上的数只是三个数中的中位数,不是所有数的中位数,不是合适的位置,换到尾部,方便后面确定位置)
0x02 分子集
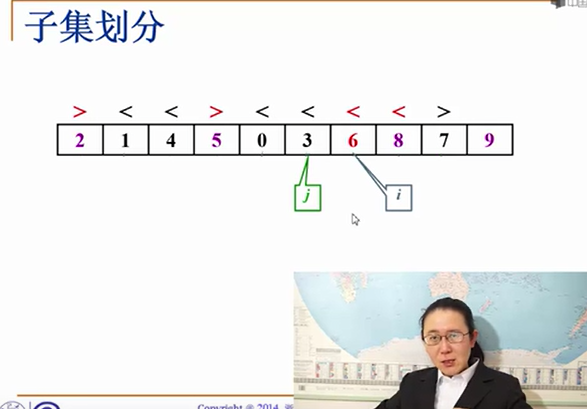
经过上面的选主元函数的处理后,集合变成如下图的样子,这时候我们用两个指针,来分子集。方法如下:
1 定义指针i,j i的初始位置为L+1(不从L开始因为选主元的函数已经确定L所在位置小于主元) 同样j的初始位置为R-2(R比主元大 R-1是主元)
2 data[i]与主元比较,如果比主元小则i++,一直循环到data[i]比主元大
3 data[j]与主元比较,如果比主元大则j–,一直循环到data[j]比主元小
4 如果i<j 那么 交换data[i] data[j]的值,使其符合要求 反之 说明已经完成了自己划分,i所在的位置就是主元应该的位置(i前面的都比主元小)所以交换主元data[R-2]与data[i] 这一步就是快速排序之所以快的原因,因为每一次递归都能确定一个元素的最终的位置,而其他诸如插入排序都是零时的位置。
这个时候已经将序列分为 左边比主元小–主元–右边比主元大 三段 ,然后对于 左 右 递归这个过程
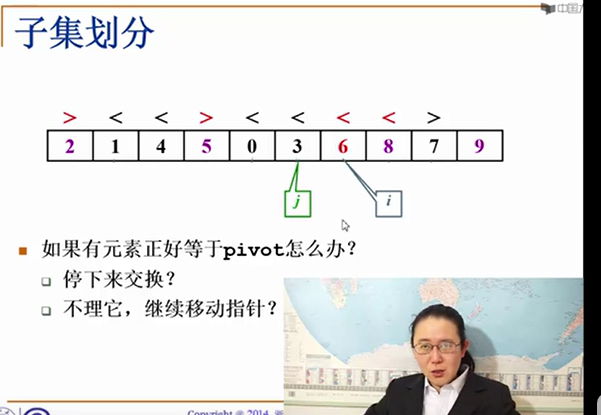
如果有元素和主元大小一样呢? 一个极端情况就是 所有元素都和主元一样大,有以下两种方案: a 上述第二步 第三步不变 严格执行 也就是如果相等,则推出第二步 第三步的循环
b 上述第二步 第三步 改成小于等于 大于等于
方法a 我们可以发现 每一次都能将序列 分成 等大的 左子列 右子列 但代价是 i 和j前进的非常慢,每次前进一步都要交换一次元素 时间复杂度为O(nlogn)
方法b 由于都相等,所以i j会一直前进 ,由于我们最后选择i的位置当主元的位置,那么最终左子列长度为n-2,右子列为1 (主元不算在其中 所以综合为n-1),这样的情况下,分子列等于没分,时间复杂度为O(n^2)
综上 我们选方案a
0x03 关于递归的优化
快速排序使用的递归 ,那么递归有个问题就是 需要占用系统堆栈,如果我们真的按照上面的伪代码描述的 一直递归分到 子序列为1才返回,那么对于较大的数据,其堆栈开销是很大的,而且在小规模数据的时候,快速递归不一定比其他排序比如选择排序快,那么,我们可以递归到子序列为某一个值的时候停止递归,直接调用其他排序来处理子序列,我们把这个值称为阈值cutoff

快速排序的时间复杂度为O(nlogn)