算法-排序

排序的本质是消除逆序对，基于交换的算法，一次交换消除的逆序对越多，速度越快。

选择排序 遍历序列，找到最小值，与第一个交换，再从第二个开始遍历，找到第二小，与第二个交换，不断重复这个过程。

时间复杂度n^2 空间 1 稳定（只交换相邻所以稳定）

**插入排序 ** 如同理牌，从第二张牌开始，都是与前面的牌一张一张比较，直到到正确的位置。

时间复杂度n^2 空间 1 稳定

**冒泡排序 ** 遍历序列，并且比较当前元素与后面一个元素大小关系，如果不符合规则，就交换，这样结束后，最大的元素就到了末尾，重复这个过程，每次遍历长度递减。（优化，如果某一次遍历交换次数为0说明已经有序，不用继续下一次遍历）

时间复杂度n^2 空间 1 稳定

希尔排序 ** 是改进的插入排序，先使用远距离比较的插入排序快速减少逆序对，然后使用小距离最终直到1的插入排序保证全部有序。把这个距离的变化成为增长序列**

时间复杂度可达n^7/6 空间 1 （不稳定）

**快速排序 ** 使用了分治的思想。确定一个主元，然后让序列的左边比主元小，右边比主元大，然后递归的处理主元左边的序列和主元右边的序列。

时间复杂度与主元的选取有关一般 nlogn 空间 logn（栈空间不稳定

**归并排序 ** 完完全全的分治思想，且是二分，要让序列有序，只要左右有序，然后合并就行，左右序列又递归前面的过程，直到长度为1。序列太长容易爆栈，非递归实现。

递归实现时间 nlogn（每次合并长度为n 递归深度logn）空间 logn 非递归时间nlogn 空间 n

**堆排序 ** 如果要从小到大排序，则建立最大堆（时间复杂度为n ）,然后不断的把堆顶的最大值与末尾交换，然后将堆的大小减1，重建堆（logn），不断重复

时间复杂度 nlogn 空间 1 不稳定（不是交换相邻）

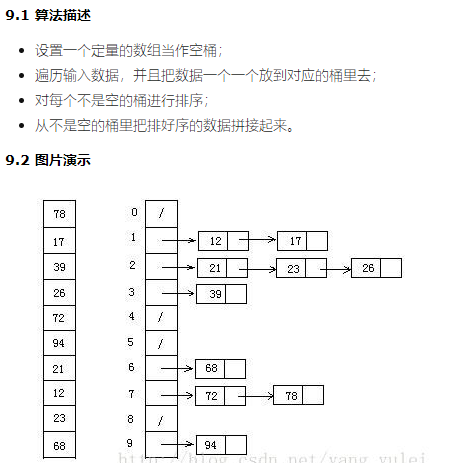
**桶排序/基数排序 ** 基数排序则是将数字从各位开始，将各位上按照0-9排序，，然后是10位（没有10位按0处理），一直到最高位被处理完就排序好了

时间复杂度 n 空间 n 稳定（不是基于比较）

TIM截图20200229101929