平衡二叉树

0x00 什么是平衡二叉树

​ 在上一节二叉搜索树中，可以发现，相同的节点集合不同的插入次序，将导致树的形状和高度不一样，导致在查找是的平均长度不一样

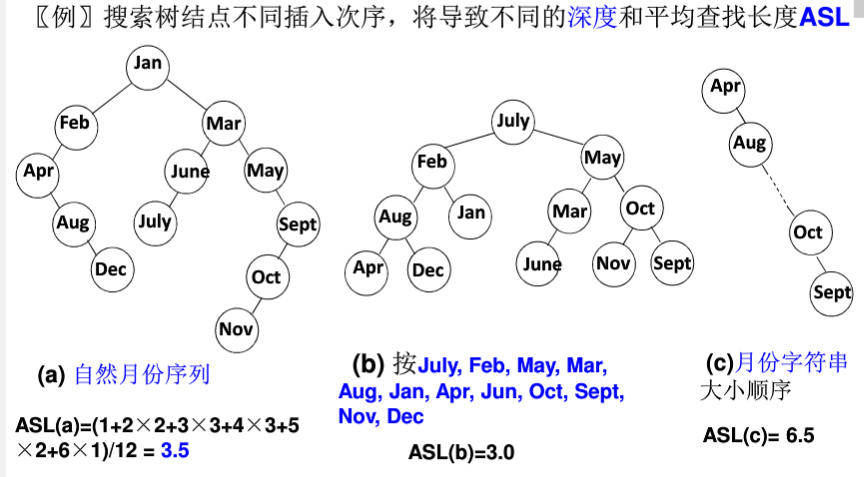
为了描述树的节点分布均匀程度，引入平衡因子这一概念：

平衡因子（balance factory 简称BF）：BF=HL-HR

​ 其中hl和hr分别为T的左子树 右子树的高度

根据平衡因子，我们定义平衡二叉树：

平衡二叉树（balance binary tree） (avl树)：空树或者任一节点的平衡因子绝对值小于1.

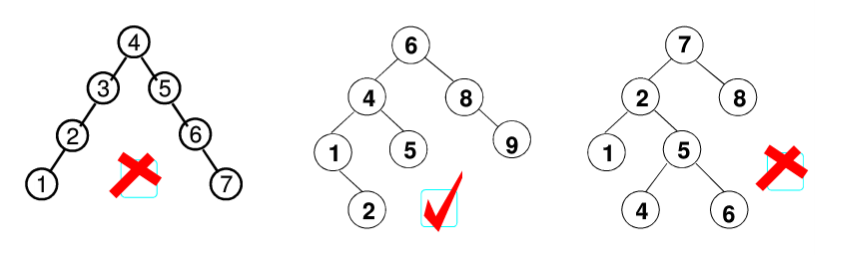
0x01 平衡二叉树性质

我们知道对于满二叉树而言，n层的节点数为2^n-1，故可知n个节点的树高近似log2n，而通过归纳法，我们也可以知道n个节点的平衡二叉树树高也近似为log2n

故可知平衡二叉树插入查找删除操作的时间复杂度均为O(logn)

0x02 平衡二叉树的调整

​ 对于一棵平衡二叉树，插入一个节点后，可能会破坏其平衡，如果不及时调整，会随着节点的增多，平衡因子越来也大，查找效率越来越低。

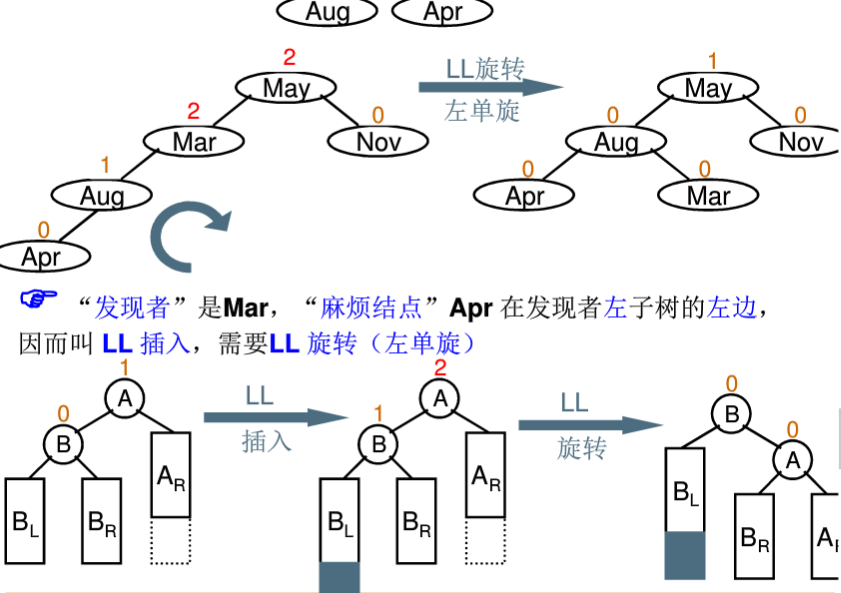
​ 在这里，把受到插入节点影响，平衡因子大于1的最靠近插入节点的那个节点称为发现者，把插入节点称为麻烦节点，根据二者的位置关系，分以下四种情况讨论：

​ RR调整：

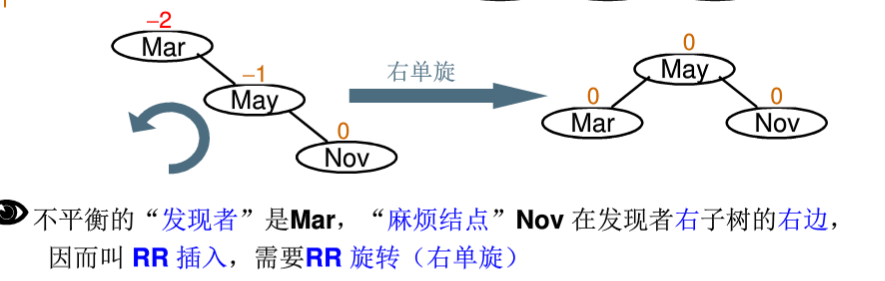
如果是下面这种情况，那么除了旋转外还要调整中间节点的子树的位置：

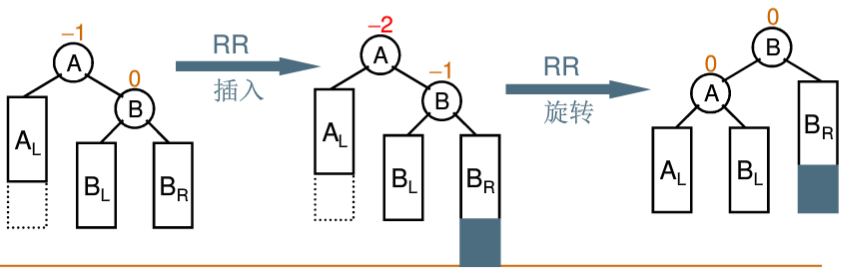
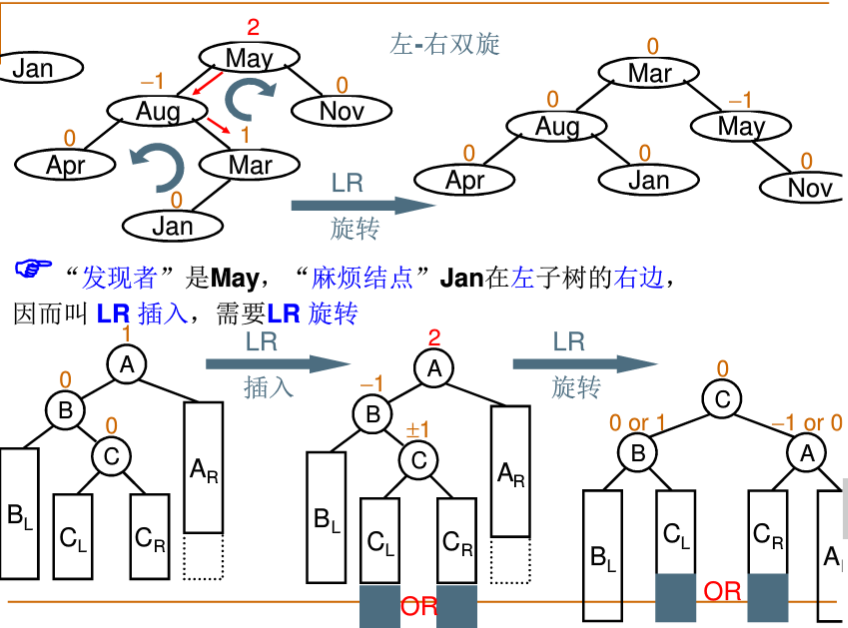
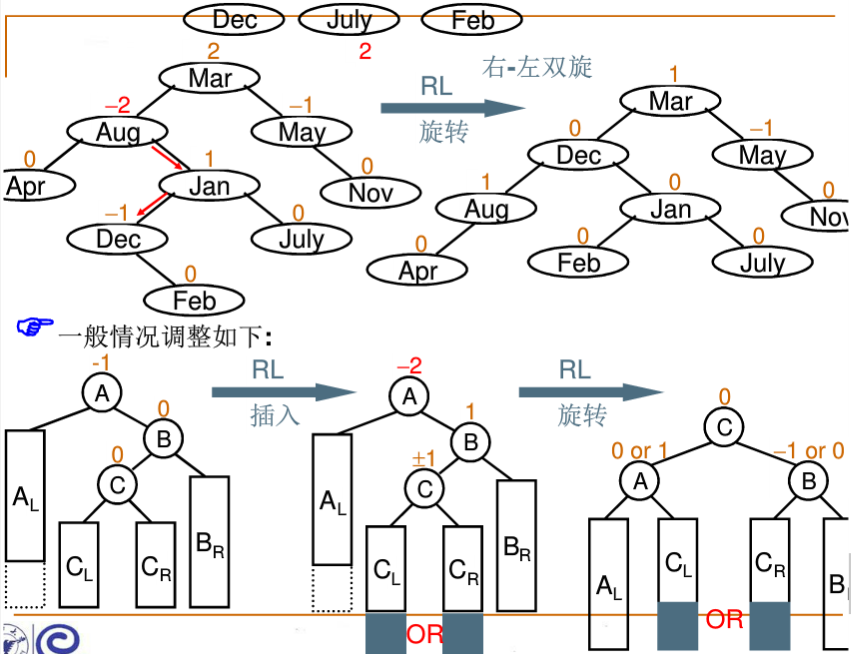
上面的调整不是很难，类似的下面三种调整思路由图片给出，代码将在下一节实现。