二叉搜索树

0x00 什么是二叉搜索树

二叉搜索树也称二叉查找树，其递归定义如下：

如果非空 1.非空右子树的所有键值大于其根节点的键值，

2非空左子树的所有键值大于其根节点的键值，

3左右子树都是二叉搜索树

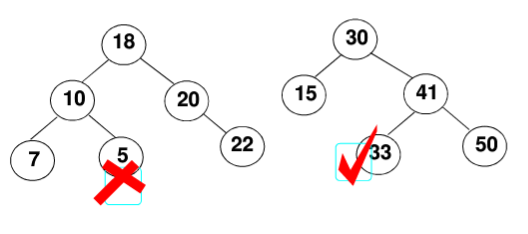
TIM截图20200203180907

二叉搜索树除了遍历外的特殊操作：

TIM截图20200203181037

0x01 二叉搜索树的基本操作

查找递归版：

node find(node p,int x){
	if(!p){
		return NULL;
	}else{
		if(x>p->data){
			return find(p->right,x);
		}else if(x<p->data){
			return find(p->left,x);
		}else{
			return p;
		}
	}
}

查找尾递归改循环版:

node find1(node p,int x){
	node ret=NULL;
	node p1=p;
	while(p1){
		if(x>p1->data){
			p1=p1->right;
		}else if(x<p1->data){
			p1=p1->left;
		}else{
			ret=p1;
			break;
		}
	}
	return ret;
}

增加节点非递归版

node add(node* p,int x){
	node ret;
	if(*p==NULL){
		(*p)=(node)malloc(sizeof(struct tnode));
		(*p)->data=x;
		(*p)->left=NULL;
		(*p)->right=NULL;
		ret=*p;
	}else{
		node p1=*p;
		while(p1){
			if(x>p1->data){
				if(p1->right){
					p1=p1->right;
				}else{
					p1->right=createnode(x);
					ret=p1->right;
					break;
				}
			}else if(x<p1->data){
				if(p1->left){
					p1=p1->left;
				}else{
					p1->left=createnode(x);
					ret=p1->left;
					break;
				}
			}else{
				ret=p1;
				printf("已有节点！");
				break;
			}
		}
	}
	return ret;
}