0x00 What is Parsing

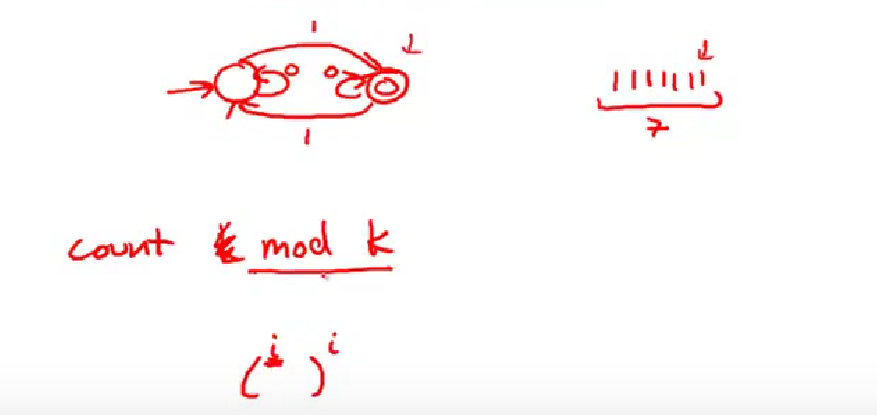
         regular languages can just match the certain string by accepting character step by step and switching from a state to another state.But regular expression can’t recognize nesting structure(like match ‘(‘ and ‘)’’ ) because there are just two state and it just switch within them and just can count it is odd or even.like the picture below:

        A parsing accept a sequnce of token which is the result producted by scaner as input and output a parsing tree for program

        what is CFG(context free grammer):We need a tool to indicate what is a valid strings of token and alse need to describe the tokens tree.So we use cfg.cfg are a natural notation for recursive structure.

        A cfg consists of:① a set of terminals T ② a set of non-terminals N ③ a start symbol S ④ a set of productions (a set of rules) X -> Y1…YN

        T N S are both grammer symbol . X->Y1…YN means you can consider Y1…YN,the symbol string, as a single X. cfg just replace left of the production with the right. the left of the production is always non-terminal,because it can be replaced by the right.

        A case to match recursive ‘(‘ ‘)’.we can replace the s with (s),and when we go on,there are the string we need match:\

        such as we need ‘( ( ) ( ) )’. the start symbol ‘s’ is replaced by epsilon .then we use’ s -> (s) ‘to make ‘epsilon ‘to ‘( epsilon)’’ . and it can alse present as ‘epsilon ( epsilon )’ .we use ‘s-> (s)’ to make it to ‘ （epsilon）(epsilon) ’ .and use it again to ‘ ( ( epsilon) (spsilon) ) ‘.finally we know epsilon is bank .So it is ‘ ( ( ) ( ) ) ‘

        so we use cfg’s rule to derive a token strings which is used to match the input token strings. If we can get the same token strings derived.

0x01 how do we derive to form a tree

        A derivation can be drawn as a tree (Parsing tree)becase there are often more than one rules match a same S.

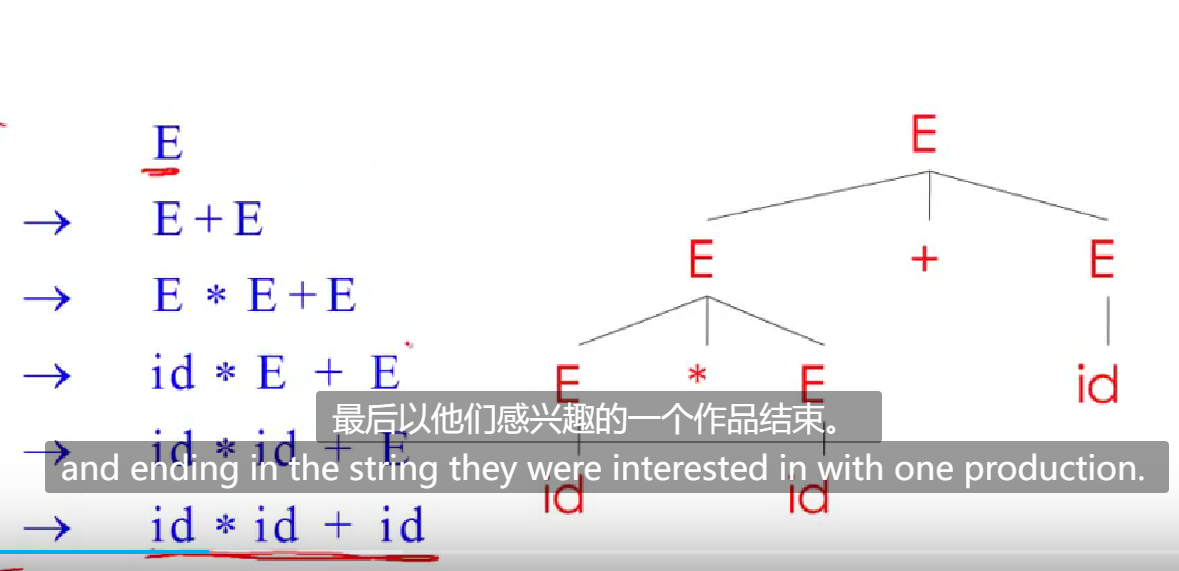
        A parsing tree’s leaves is terminal and other node is non-terminal.and the sub tree will get a higher priority of handle than it’s parent.

        Because there are more than one child node,so when we derive the tree by cfg’s rule,there are two way:①left-most,at each step,replace the left-most non-terminal ②right-most,on the contrary

        So,there are more than one dervivation,one of it is we nedd.It call ambiguity.

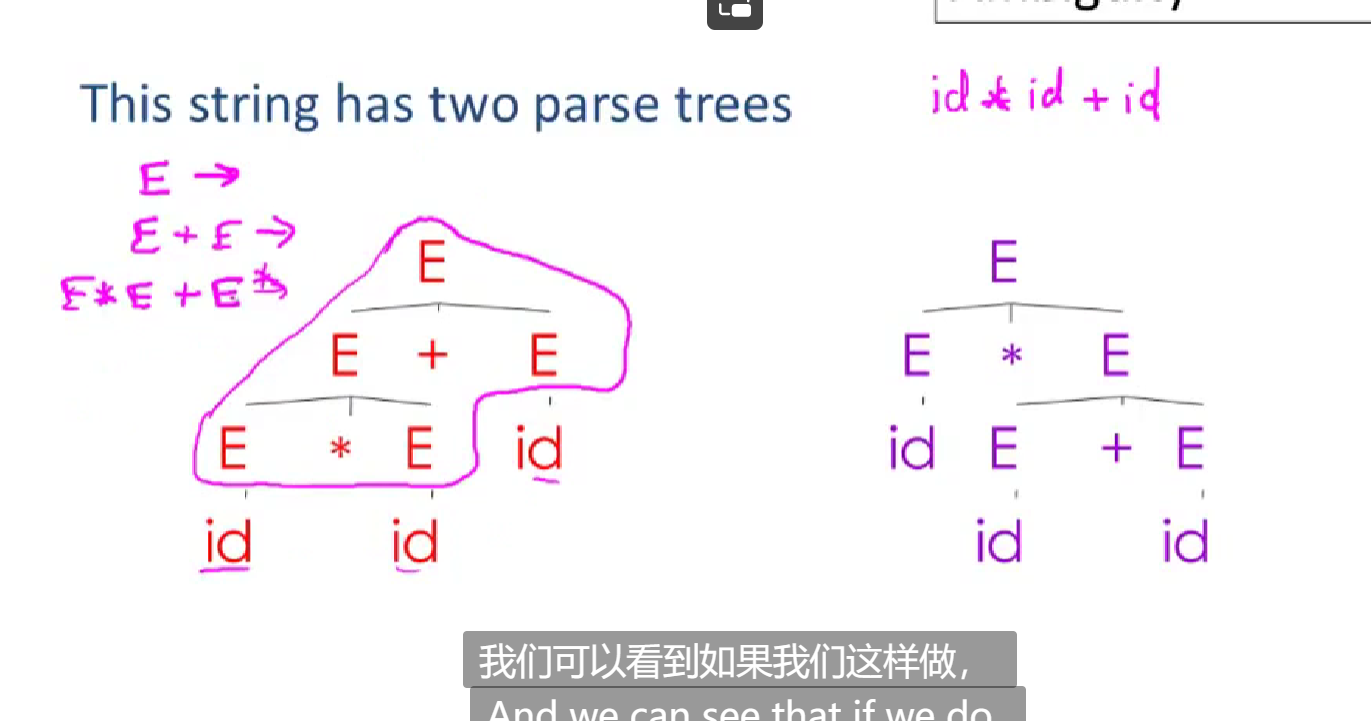
        As we know,we need handle the plus first than times when there are no ().So when we use right-most,we get wrong derivation. A grammar is ambiguous if it has more than one parse tree for some string,because it get wrong handle order for parsing tree.Ambiguity is bad!

        there are several ways to handle ambiguity:①rewrite grammar .such as use E to handle plus,and use E’ to handle times.we note that E’ can also be replaced by (E) to implent (1+2) * 3

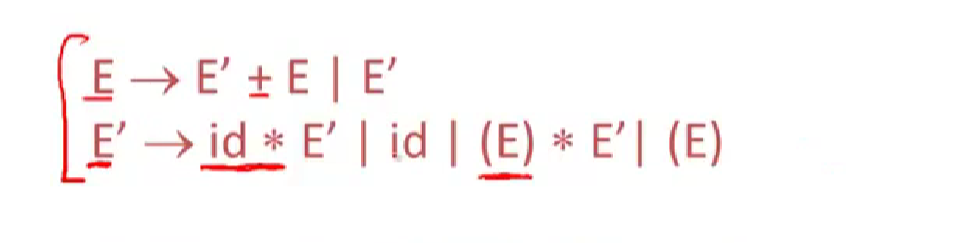
        ②enforce precedence of * over +

        another ambiguity:if then else,we want else match the closest then.

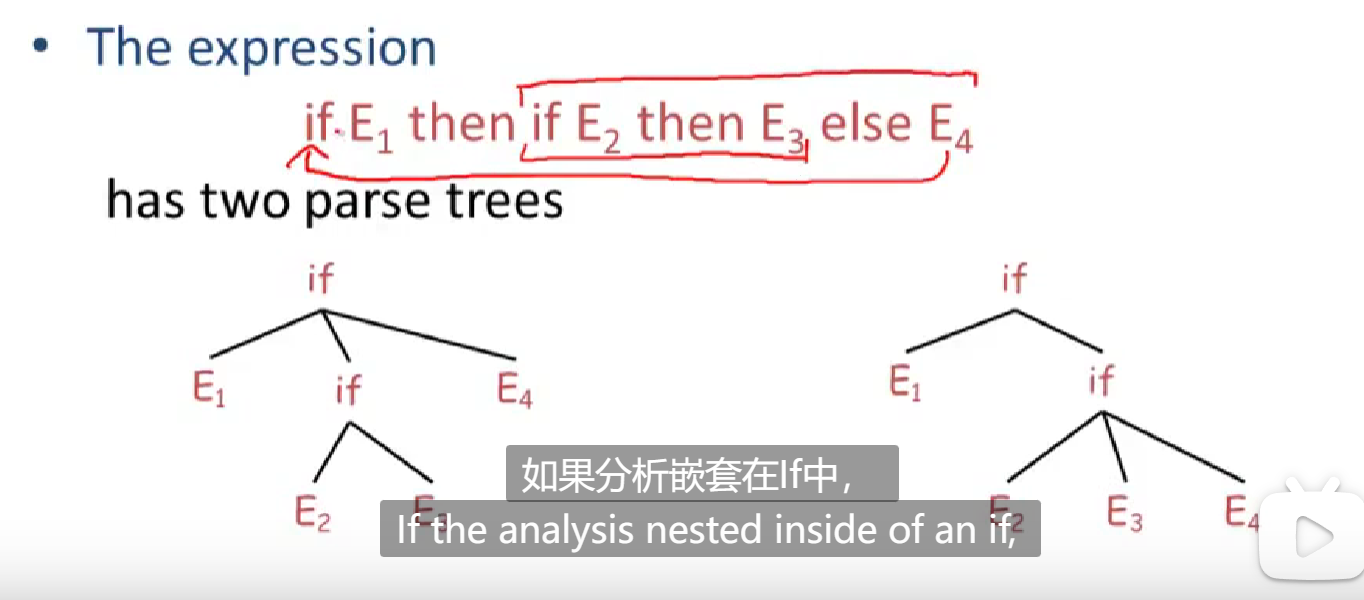
        alse can rewrite grammer like this:

        rewrite grammer make itself more complex and confused.Most tools allow precedence and associativity declarations to disambiguate grammars.

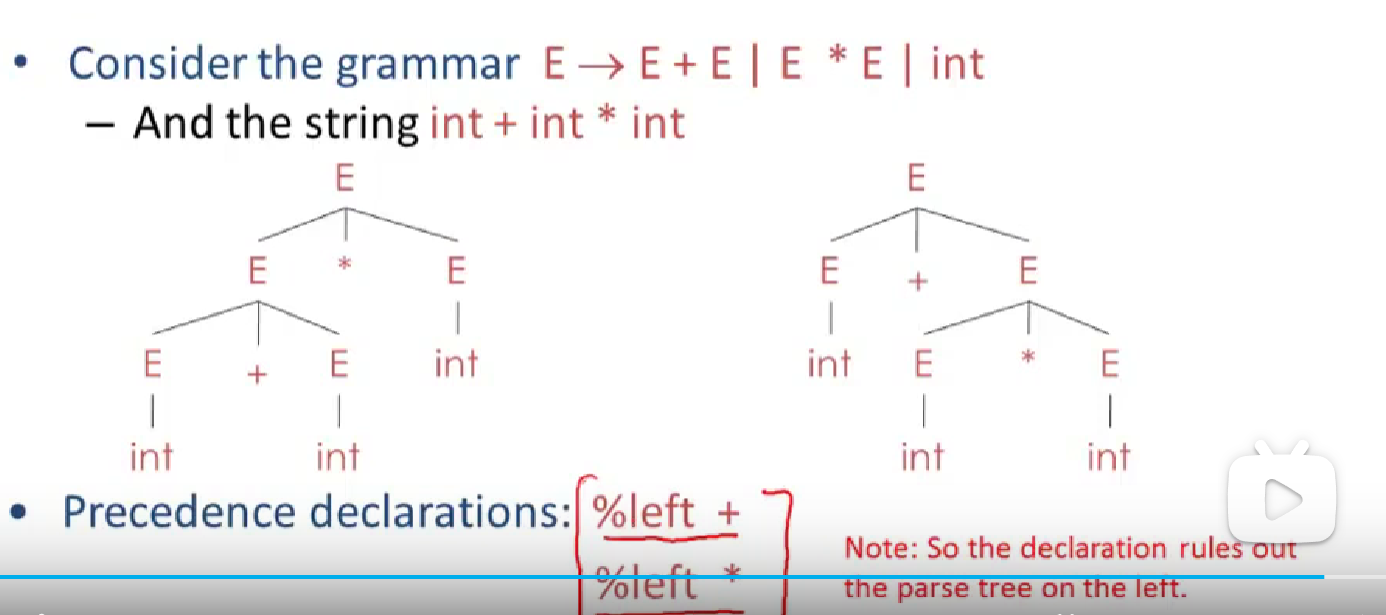
        in bison,we use %left + to declare associate left first in plus,and the later %left * means times has higer precedence than plus.

0x02 Error Handling

        kinds of errors:

        Error handler should:①report errors ②recover from error ③not slow down compilation

        there are three way to handle error:①panic mode ②error productions ③automatic correction.We often use the two of the former.

        Panic mode when detect error,parser begain discard tokens til it coform correct rules.This is the most popular strategy.

        the second + will be discarded and the 2 will be accepted.In Bison,use the special terminal error to describe how much input to skip:   

       Error productions specify known common mistakes in the grammar.(we konow it is error,but we just accept it by specify special productions/rules precedely).

        Automatic correction:find a correct “nearby” program.It was useful when we cost much time in compilation.

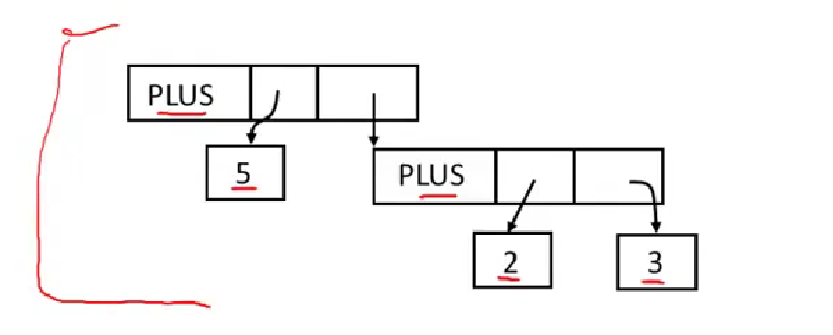
0x03 Abstract syntax tree

        We need ast to simplify parse tree.

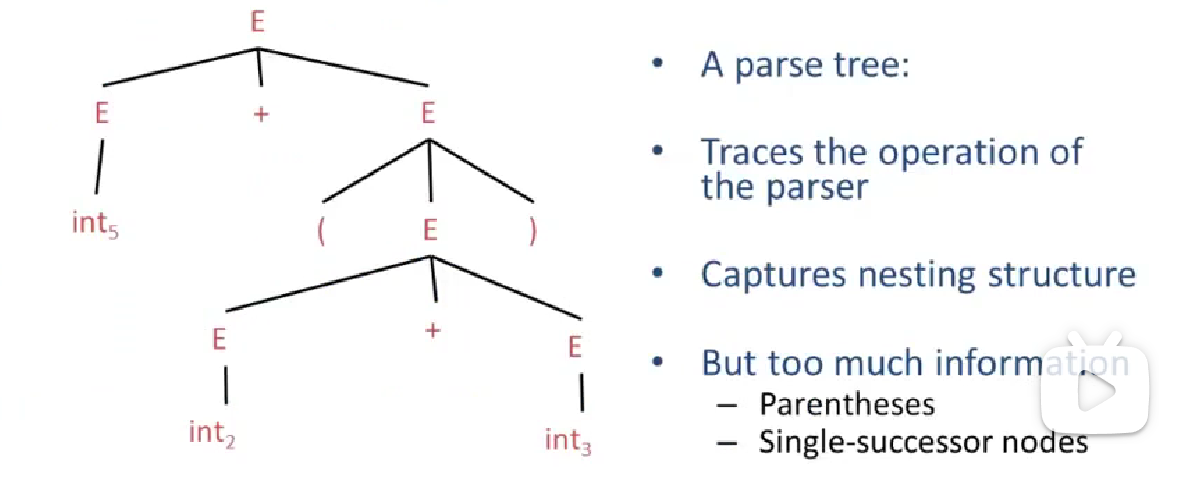
        This is ast,it abstracts from the concrete syntax