散列表的冲突解决方法
散列表的冲突解决方法
0x00 思路
常用的处理冲突的思路:
换个位置:
同一位置的冲突对象组织在一起 链地址法
0x01 开放定址法(open addressing)

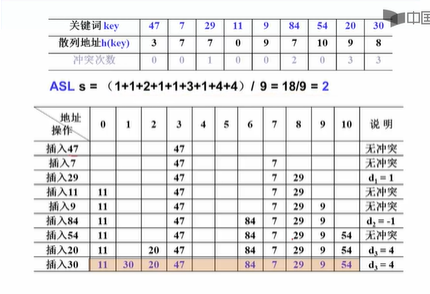
线性探测:
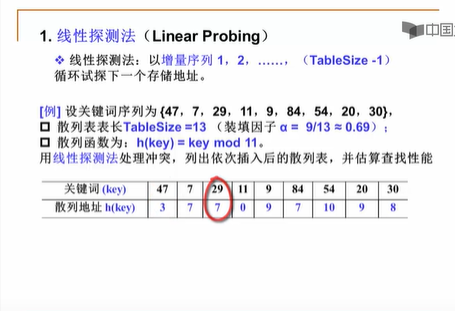
线性探测的插入: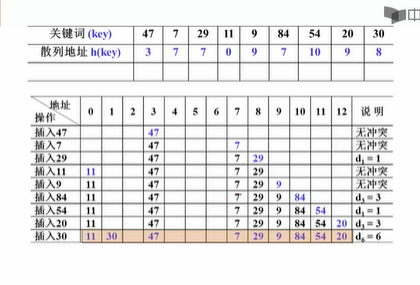
很简单就是冲突了(散列地址已经有元素了,就往下一个位置,一直到遇到空位置)
线性探测 查找性能分析: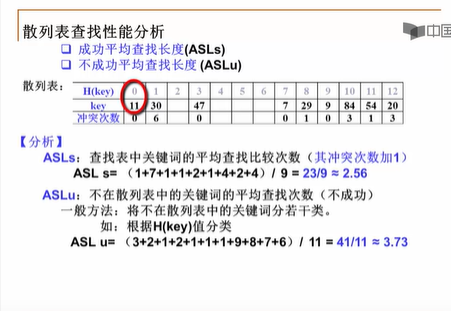
不成功查找次数是按类来分的,比如22 和 33 求的地址都是0,但是地址0上已经有11了,所以会冲突,一直往前两次发现空位,还没找到22或33 才说明查找失败了,所以余数为零(地址求的为0的)不成功查找次数都是3 其余地址的一样的算
线性探测会出现聚集现象,就是一旦有冲突,就会聚集在一起,形成正反馈,不断加剧聚集现象。
字符串的线性探测

平方探测:
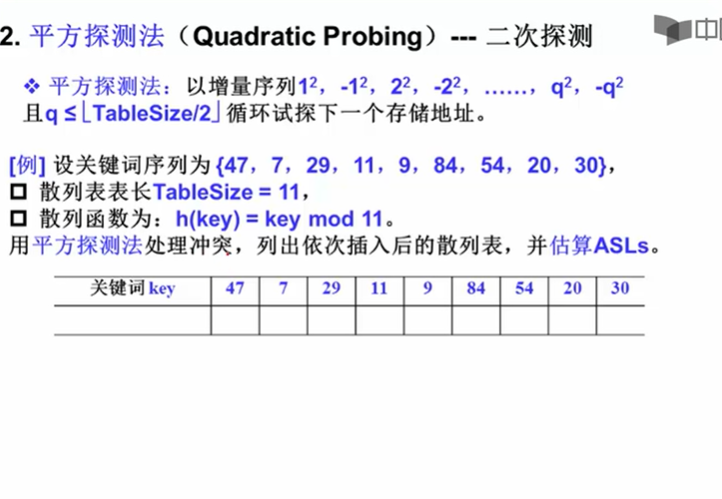
第i此冲突的增量是 i%2==1,di= ((i+1)/2)^2 i%2==0,di=(i/2)^2
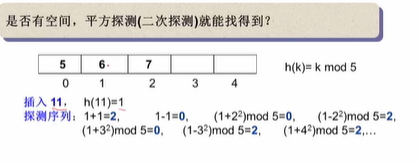
是否有空位,平方探测可能找不到?(因为每次改变的位置是平方,而且有时候加有时候减,即使取余后也不在空位上)
这种现象有可能发生:
二次探测也有聚集现象,但没有线性探测严重。且有定理显示,如果散列表的长度tablesize(也就是取余的p)是某个4k+3(k是正整数)形式的素数时,平方探测法就可以探查到整个散列空间
