基于博弈树的五子棋ai
随手写的五子棋(博弈树)
0x00 评估函数
这是最最基本的,我们想要让我们的ai能够正常下棋,就必须能够对局面进行一个定量的评估,指导什么是好局面,什么是坏局面,这有这样才可能使局面越来越好。
对于五子棋,我们主要考虑以下可能 成五(已经赢了,最好局面) 双活四(四子相连,且头尾两边都有空位,极大可能性转化成五,给分低于成五一个量级,但也非常高)单活四(四子相连,只有一边有空位,有记录转化成五,给分低于双活四一个量级) 双活三 双活二 同样的分数量级一个比一个低。其余不得分。于是对于一种花色的棋子,其评估函数如下:
int getvalue(int *data,int flag){
int i,j,k;
int len1=0,len2=0;
int val[5]={0,0,0,0,0};
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]=4;
for(k=1;k<=4;k++){
if(j+k<maplen&&data[i*maplen+j+k]==flag){
data[i*maplen+j+k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(j-k>=0&&data[i*maplen+j-k]==flag){
data[i*maplen+j-k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[3]++;
if(len1+len2==3&&(!(j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==3&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&!(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==2&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[1]++;
if(len1+len2==1&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&data[(i+k)*maplen+j]==flag){
data[(i+k)*maplen+j]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&data[(i-k)*maplen+j]==flag){
data[(i-k)*maplen+j]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&!(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&j-k>=0&&data[(i+k)*maplen+j-k]==flag){
data[(i+k)*maplen+j-k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&j+k<maplen&&data[(i-k)*maplen+j+k]==flag){
data[(i-k)*maplen+j+k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&!(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&j+k<maplen&&data[(i+k)*maplen+j+k]==flag){
data[(i+k)*maplen+j+k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&j-k>=0&&data[(i-k)*maplen+j-k]==flag){
data[(i-k)*maplen+j-k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&!(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
return val[4]?10000:0+val[3]?1000:0+val[2]?100:0+val[1]?10:0+val[0]?1:0;
}
需要注意的是,五子棋是一种零和博弈,上述函数只给出了一方棋子的评估分数,一方实际分数=己方评估分数-对方评估分数
0x01 博弈树
如果我们只着眼于当前局面,来制定下一步棋的策略,显然是不够聪明的,当前最优不一定是全局最优,所以我们(不论是人类还是机器)都会多思考几层,类似 我这一步可以下哪些地方,对手针对我下的地方又会对应的下哪些地方,所以,为了能够赢棋,我们需要多思考几步,从几步之后的局面,反推回来我们现在该怎么走。
那么在这个思考的过程中,我们每次站在自己的角度想的时候,都是给自己想的最好局面,而站在对手角度想都是给自己最坏的局面,所以如果我们用一棵树来表示我们的思考过程,应该如下:
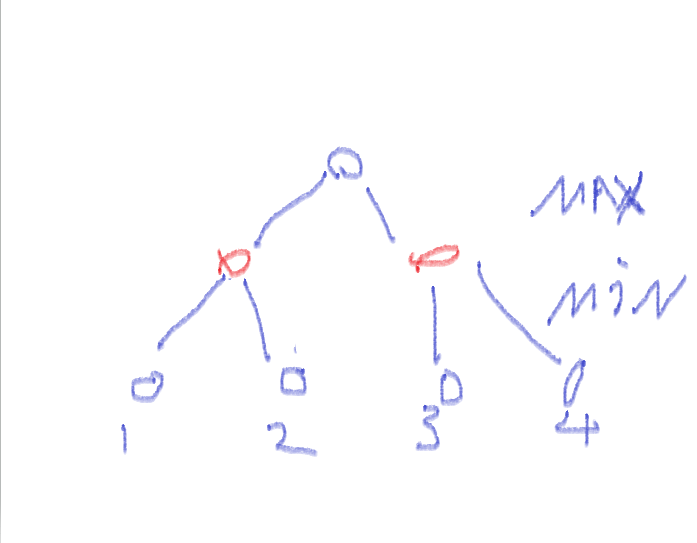
我们假设当前情况是根节点,轮到我们下下一步棋,简化问题为不论我还是对手,每一次都只有两种走法,那么我们在根节点思考两层,也就是往下扩展我们的博弈树,到了根节点层,也就是我们本次思考的终点,我们需要看一下两步过后的每一个局面,用上面的评估函数对每个根节点进行打分,假设分数分别是1,2,3,4。那么,我们往前推,前一层是对手的回合,比如对手站在第一个红色节点的局面来分析,下一步有两种情况 ,分别让我得分是1和2,那对手会选择对我不利的1,所以我们认为第一个红色节点分数实际是1,同样的第二个节点是3,我们把由对手决定的,选择最小结果的一层称为min层,反过来我们选择的,结果最大的一层我们称为max层,所以我们在根节点时应该做出的决策 变成第二红色节点的局面。这个过程就是博弈树。其函数实现如下:
int maxmin(int depth,int*data,int flag,int a,int b){
if(!depth){
return getvalue(data,1)-getvalue(data,-1);
}
if(flag==1){//轮到自己走了,选最大的
ch p=getchild(data,flag);
ch p1=p->next;
while(p->next){
int tmp=maxmin(depth-1,p->next->ls,flag*(-1),a,b);
if(tmp>a) {
a=tmp;
if(a>b) break;
if(depth==dddd){
int i;
for(i=0;i<mapsize;i++){
data[i]=p->next->ls[i];
}
}
}
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
while(p->next){
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
free(p->ls);
free(p);
return a;
}else{
ch p=getchild(data,flag);
ch p1=p->next;
while(p->next){
int tmp=maxmin(depth-1,p->next->ls,flag*(-1),a,b);
if(tmp<b){
b=tmp;
if(a>b) break;
}
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
while(p->next){
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
free(p->ls);
free(p);
return b;
}
}
上面的代码是带剪枝的,伪代码描述是:
int maxmin(root,depth,flag)//root储存局面 depth 是深度 用来判断是不是根节点 flag用来判断 是max层还是min层
{
if(depth==0){ return getvalue(我)-getvlaue(对手);
}
if (flag==我){
max=-100000
对于每个子节点:
tmp=maxmin(子节点,depth-1,对方)
if(tmp>max) {
max=tmp;
if(depth==刚开始的depth){
在这里就可以拿到根节点时,最好的子节点
}
}
return max;
}else if(flag=对方){
min=100000
对于每个子节点:
tmp=maxmin(子节点,depth-1,我)
if(tmp<min) max=tmp;
return min;
}
}
0x02 alpha beta剪枝算法
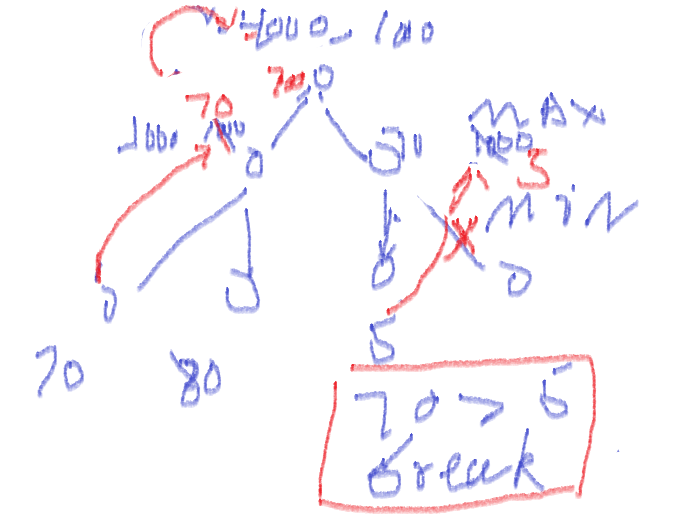
由于时间关系 不再说明,实际上该剪枝算法是通过对maxmin博弈树的分析,找到的规律,通过每个节点的上下界的形式,来判断后面的子节点是不是还有必要遍历
0x03 全代码如下
dddd是思考层数 dis是每一步落子的位置于场上棋子位置的距离,越大每一步可能的位置就
越多,程序也就越慢
#include <stdio.h>
#include <stdlib.h>
#define mapsize 225
#define maplen 15
#define dddd 3
#define dis 1
typedef struct tnode* node;
typedef struct child* ch;
struct child{
int*ls;
ch next;
};
void print_map(int* data){
int i,j;
printf("\t 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 \n");
printf("\t ———————————————\n");
for(i=0;i<maplen;i++){
printf("%d\t|",i);
for(j=0;j<maplen;j++){
switch(data[i*maplen+j]){
case 0:
printf(" ");
break;
case 1:
printf("X ");
break;
case -1:
printf("O ");
break ;
}
}
printf("|");
printf("\n");
}
printf("\t ———————————————\n");
}
ch getchild(int* data,int flag){
ch ret=(ch)malloc(sizeof(struct child));
ret->next=NULL;
ret->ls=(int*)malloc(sizeof(int)*mapsize);
ch p=ret;
int i,j,m,n,x,y;
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==1||data[i*maplen+j]==-1){
for(m=i-dis;m<=i+dis;m++){
if(m>=0&&m<maplen)
for(n=j-dis;n<=j+dis;n++){
if(n>=0&&n<maplen)
if(data[m*maplen+n]==0){
ch tmp=(ch)malloc(sizeof(struct child));
tmp->ls=(int*)malloc(sizeof(int)*mapsize);
tmp->next=NULL;
p->next=tmp;
p=tmp;
for(x=0;x<maplen;x++){
for(y=0;y<maplen;y++){
if(x==m&&y==n) tmp->ls[x*maplen+y]=flag;
else tmp->ls[x*maplen+y]=data[x*maplen+y];
}
}
}
}
}
}
}
}
if(ret->next==NULL){
ch tmp=(ch)malloc(sizeof(struct child));
tmp->ls=(int*)malloc(sizeof(int)*mapsize);
tmp->next=NULL;
ret->next=tmp;
int i;
for(i=0;i<mapsize;i++){
if(i>mapsize/2-1&&i<mapsize/2+1&&data[i]==0)tmp->ls[i]=flag;
else tmp->ls[i]=data[i];
}
}
return ret;
}
int getvalue(int *data,int flag){
int i,j,k;
int len1=0,len2=0;
int val[5]={0,0,0,0,0};
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]=4;
for(k=1;k<=4;k++){
if(j+k<maplen&&data[i*maplen+j+k]==flag){
data[i*maplen+j+k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(j-k>=0&&data[i*maplen+j-k]==flag){
data[i*maplen+j-k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[3]++;
if(len1+len2==3&&(!(j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==3&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&!(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==2&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[1]++;
if(len1+len2==1&&((j+len1+1<maplen&&data[i*maplen+j+len1+1]==0)&&(j-len2-1>=0&&data[i*maplen+j-len2-1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&data[(i+k)*maplen+j]==flag){
data[(i+k)*maplen+j]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&data[(i-k)*maplen+j]==flag){
data[(i-k)*maplen+j]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&!(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&data[(i+len1+1)*maplen+j]==0)&&(i-len2-1>=0&&data[(i-len2-1)*maplen+j]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&j-k>=0&&data[(i+k)*maplen+j-k]==flag){
data[(i+k)*maplen+j-k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&j+k<maplen&&data[(i-k)*maplen+j+k]==flag){
data[(i-k)*maplen+j+k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&!(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&j-len1-1>=0&&data[(i+len1+1)*maplen+j-len1-1]==0)&&(i-len2-1>=0&&j+len2+1<maplen&&data[(i-len2-1)*maplen+j+len2+1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==flag){
len1=0;
len2=0;
data[i*maplen+j]==4;
for(k=1;k<=4;k++){
if(i+k<maplen&&j+k<maplen&&data[(i+k)*maplen+j+k]==flag){
data[(i+k)*maplen+j+k]=4;
len1++;
}
}
for(k=1;k<=4;k++){
if(i-k>=0&&j-k>=0&&data[(i-k)*maplen+j-k]==flag){
data[(i-k)*maplen+j-k]=4;
len2++;
}
}
if(len1+len2==4) val[4]++;
if(len1+len2==3&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[3]++;
if(len1+len2==3&&(!(i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==3&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&!(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[2]++;
if(len1+len2==2&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[1]++;
if(len1+len2==1&&((i+len1+1<maplen&&j+len1+1<maplen&&data[(i+len1+1)*maplen+j+len1+1]==0)&&(i-len2-1>=0&&j-len2-1>=0&&data[(i-len2-1)*maplen+j-len2-1]==0))) val[0]++;
}
}
}
for(i=0;i<maplen;i++){
for(j=0;j<maplen;j++){
if(data[i*maplen+j]==4){
data[i*maplen+j]=flag;
}
}
}
return val[4]?10000:0+val[3]?1000:0+val[2]?100:0+val[1]?10:0+val[0]?1:0;
}
int maxmin(int depth,int*data,int flag,int a,int b){
if(!depth){
return getvalue(data,1)-getvalue(data,-1);
}
if(flag==1){//轮到自己走了,选最大的
ch p=getchild(data,flag);
ch p1=p->next;
while(p->next){
int tmp=maxmin(depth-1,p->next->ls,flag*(-1),a,b);
if(tmp>a) {
a=tmp;
if(a>b) break;
if(depth==dddd){
int i;
for(i=0;i<mapsize;i++){
data[i]=p->next->ls[i];
}
}
}
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
while(p->next){
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
free(p->ls);
free(p);
return a;
}else{
ch p=getchild(data,flag);
ch p1=p->next;
while(p->next){
int tmp=maxmin(depth-1,p->next->ls,flag*(-1),a,b);
if(tmp<b){
b=tmp;
if(a>b) break;
}
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
while(p->next){
free(p->ls);
free(p);
p=p1;
p1=p1->next;
}
free(p->ls);
free(p);
return b;
}
}
void getnextstep(int*a,int*b,int*map){
while(scanf("%d%d",a,b)!=2||*a<0||*a>=maplen||*b<0||*b>=maplen||map[*a*maplen+*b]){
gets(NULL);
printf("输入有误!请重新输入位置x,y(从0-%d)\n",maplen-1);
}
}
int trans(int x,int y){
return x*maplen+y;
}
int main(void){
int map[mapsize]={0};
while(1){
maxmin(dddd,map,1,-100000,100000);
print_map(map);
if(getvalue(map,1)>=10000){
printf("ai win!\n");
break;
}
int x,y;
getnextstep(&x,&y,map);
map[x*maplen+y]=-1;
print_map(map);
if(getvalue(map,-1)>=10000){
printf("you win!\n");
break;
}
}
return 0;
}
