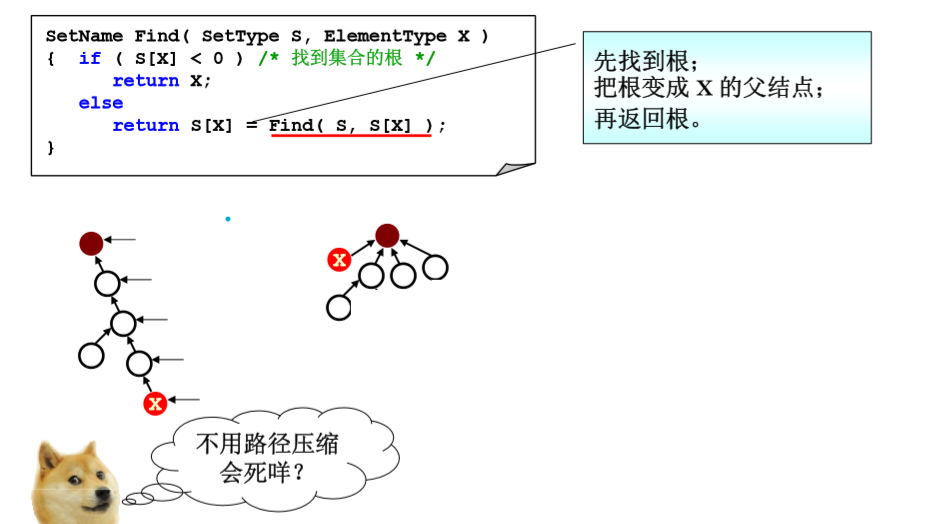
集合运算例题
File Transfer
0x00 集合的简化表示
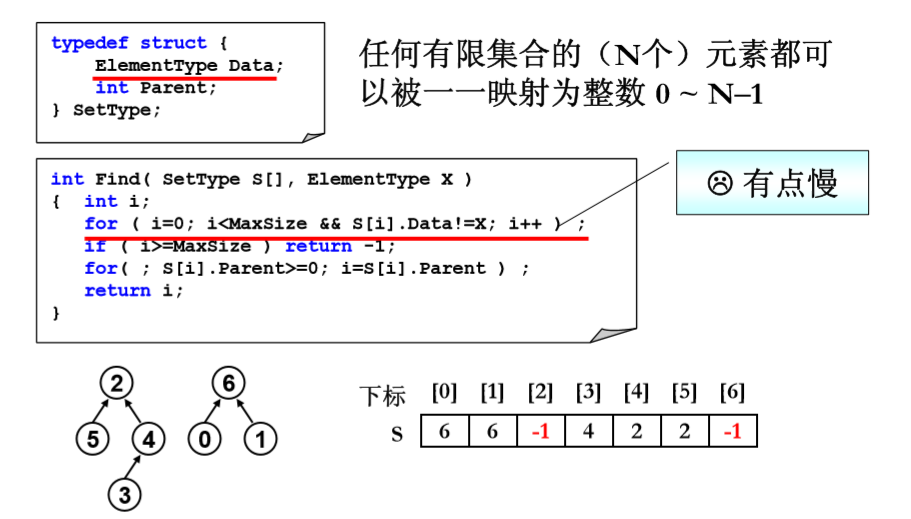
在之前 我们用一个自定义结构数组来储存一个集合树,所以我们在一个元素的根节点的时候,必然先要便利数组,先找到这个元素,再找其根节点,那么对于n个节点,其时间复杂度是O(N^2),所以必须改进。
改进的办法就是,我们不开辟空间来储存元素,而是用数组下标来表示或者说映射元素,那么,每次需要找到某个节点,只需要提供对应的i就是了。在本题中,我们的元素事先被编号了,那么编号-1,即是其下标,下标+1,即是对应元素。在找到元素这一项任务上n个元素时间复杂度是O(N)。

0x01 题目描述
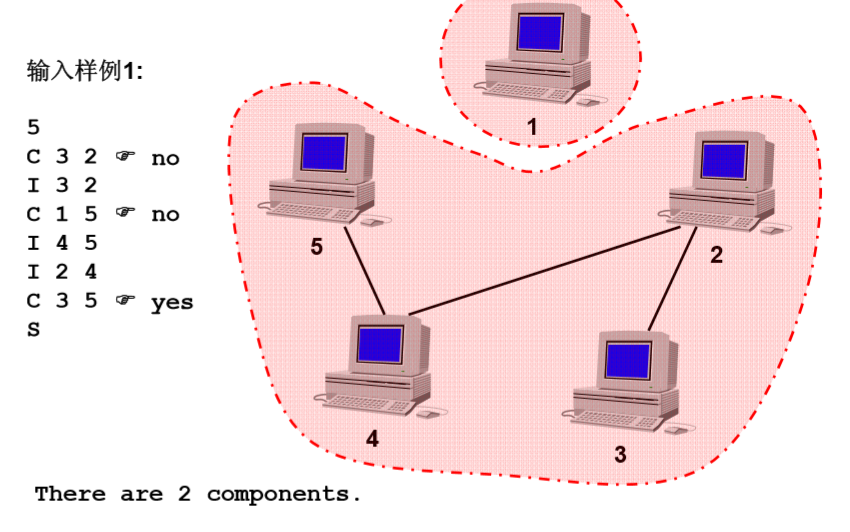 第一行代表元素个数
第一行代表元素个数
后面的每一行, 第一个是指令 后面两个 是元素 C 是check 查询两个主机是否相连,也就是是否在同一个集合,I是input_connection 将两个主机连在一起,也就是合并集合(如果不是在一个集合的话),S则是结束。
要求在每条C指令后面输出是否连通,S后署出一个有几个连通分量。
0x02 代码实现
#include <stdio.h>
#include <stdlib.h>
int find(int *data,int x){
int ret=x;
while(data[ret]>0){
ret=data[ret];
}
return ret;
}
void un(int* data,int a,int b){
int root1=find(data,a);
int root2=find(data,b);
if(root1!=root2){
data[root2]=root1;
}
}
int main(){
int m;
int i;
int a,b;
scanf("%d",&m);
getchar();
int* data=(int*)malloc(sizeof(int)*m);
for(i=0;i<m;i++){
data[i]=-1;
}
char C;
do{
scanf("%c",&C);
switch (C){
case 'C':{
scanf("%d %d",&a,&b);
getchar();
if(find(data,a-1)==find(data,b-1)) printf("yes\n");
else printf("no\n");
break;
}
case 'I':{
scanf("%d %d",&a,&b);
getchar();
un(data,a-1,b-1);
break;
}
case 'S':{
int cnt=0;
for(i=0;i<m;i++){
if(data[i]<0){
cnt++;
}
}
printf("there are %d components.",cnt);
break;
}
}
}while(C!='S');
return 0;
}
以上代码测试通过
0x03 性能优化
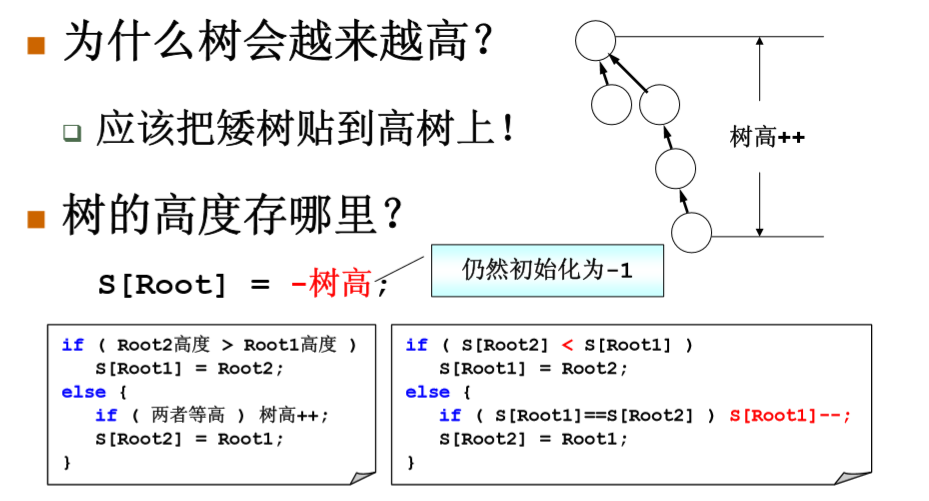
在上面的代码 un函数(并集函数)中,总是简单的将root2的父节点设置位root1,这样做有个问题,就是树的高度会不断增加,有可能使find 变成O(n^2)。 所以我们得引入按秩归并


另外一个优化的方式就是,在find函数中 我们把我们要找的元素的根节点找到后,直接设置为该元素的父节点,这种优化方式称为路径压缩
下图的路径压缩是尾递归方式实现的,其实可以用循环。